PROBABILITAS DAN TEORI BAYES
PENGERTIAN PROBABILITAS

Pengertian Probabilitas adalah suatu nilai yang digunakan untuk
mengukur tingkat terjadinya suatu kejadian yang acak. Kata probabilitas
itu sendiri sering disebut dengan peluang atau kemungkinan. Probabilitas
secara umum merupakan peluang bahwa sesuatu akan terjadi.
Konsep probabilitas memiliki peranan yang penting dalam kehidupan
sehari-hari, mulai dari bidang ilmiah, bidang pemerintahan, bidang
usaha atau industri, sampai pada masalah-masalah kecil seperti masuk
kantor atau tidak karena awan tebal yang kemungkinan akan hujan deras
dan banjir.
Dalam mempelajari probabilitas, ada tiga kata kunci yang harus diketahui yaitu eksperimen, hasil (outcome) dan kejadian atau peristiwa (even).
Sebagai contoh, sebuah eksperiman dilakukan dengan menanyakan kepada
100 orang pembaca, apakah mereka akan mengambil mata kuliah statistik
atau kalkulus. Dari eksperimen ini akan terdapat beberapa kemungkinan
hasil. Contohnya kemungkinan hasil pertama ialah sebanyak 58 orang akan
mengambil mata kuliah apapun. Kemungkinan hasil lain adalah bahwa 75
orang mengambil mata kuliah kalkulus dan sisanya mengambil mata kuliah
statistik. Contoh lain dari eksperimen adalah pelemparan sebuah dadu.
Hasil (outcome) dari pelemparan sebuah dadu tersebut kemungkian
akan keluar biji satu atau biji dua atau biji tiga dan seterusnya.
Kumpulan dari beberapa hasil tersebut dikenal sebagai kejadian (even).
Probabilitas biasanya dinyatakan dengan bilangan desimal (seperti
0,50, 0,20 atau 0,89) atau bilangan pecahan seperti 5/100, 20/100,
75/100. Nilai dari probabilitas berkisar antara 0 sampai dengan 1. Jika
semakin dekat nilai probabilitas ke nilai 0, maka semakin kecil juga
kemungkinan suatu kejadian akan terjadi. Jika semakin dekat nilai
probabilitas ke nilai 1, maka semakin besar peluang suatu kejadian akan
terjadi.
Teorema Bayes
Dalam teori probabilitas dan statistika,
teorema Bayes adalah sebuah teorema dengan dua penafsiran berbeda. Dalam penafsiran Bayes, teorema ini menyatakan seberapa jauh derajat kepercayaan subjektif harus berubah secara rasional ketika ada petunjuk baru. Dalam penafsiran frekuentis teorema ini menjelaskan representasi invers probabilitas dua kejadian. Teorema ini merupakan dasar dari statistika Bayes dan memiliki penerapan dalam sains, rekayasa, ilmu ekonomi (terutama ilmu ekonomi mikro), teori permainan, kedokteran dan hukum. Penerapan teorema Bayes untuk memperbarui kepercayaan dinamakan inferens Bayes.
teorema Bayes adalah sebuah teorema dengan dua penafsiran berbeda. Dalam penafsiran Bayes, teorema ini menyatakan seberapa jauh derajat kepercayaan subjektif harus berubah secara rasional ketika ada petunjuk baru. Dalam penafsiran frekuentis teorema ini menjelaskan representasi invers probabilitas dua kejadian. Teorema ini merupakan dasar dari statistika Bayes dan memiliki penerapan dalam sains, rekayasa, ilmu ekonomi (terutama ilmu ekonomi mikro), teori permainan, kedokteran dan hukum. Penerapan teorema Bayes untuk memperbarui kepercayaan dinamakan inferens Bayes.
Pengenalan
Misalkan kawan Anda bercerita dia bercakap-cakap akrab dengan seseorang lain di atas kereta api. Tanpa informasi tambahan, peluang
dia bercakap-cakap dengan perempuan adalah 50%. Sekarang misalkan kawan
Anda menyebut bahwa orang lain di atas kereta api itu berambut panjang.
Dari keterangan baru ini tampaknya lebih bolehjadi kawan Anda
bercakap-cakap dengan perempuan, karena orang berambut panjang biasanya
wanita. Teorema Bayes dapat digunakan untuk menghitung besarnya peluang
bahwa kawan Anda berbicara dengan seorang wanita, bila diketahui berapa
peluang seorang wanita berambut panjang.
Misalkan:
- W adalah kejadian percakapan dilakukan dengan seorang wanita.
- L adalah kejadian percakapan dilakukan dengan seorang berambut panjang
- M adalah kejadian percakapan dilakukan dengan seorang pria
Kita dapat berasumsi bahwa wanita adalah setengah dari populasi. Artinya peluang kawan Anda berbicara dengan wanita,
Misalkan juga bahwa diketahui 75 persen wanita berambut panjang. Ini
berarti bila kita mengetahui bahwa seseorang adalah wanita, peluangnya
berambut panjang adalah 0,75. Kita melambangkannya sebagai:
Sebagai keterangan tambahan kita juga mengetahui bahwa peluang seorang pria berambut panjang adalah 0,3. Dengan kata lain:
Di sini kita mengasumsikan bahwa seseorang itu adalah pria atau wanita, atau P(M) = 1 - P(W) = 0,5. Dengan kata lain M adalah kejadian komplemen dari W.
Tujuan kita adalah menghitung peluang seseorang itu adalah wanita
bila diketahui dia berambut panjang, atau dalam notasi yang kita
gunakan, P(W|L). Menggunakan teorema Bayes, kita mendapatkan:
Di sini kita menggunakan aturan peluang total.
Dengan memasukkan nilai-nilai peluang yang diketahui ke dalam rumus di
atas, kita mendapatkan peluang seseorang itu wanita bila diketahui dia
berambut panjang adalah 0,714. Angka ini sesuai dengan intuisi awal
kita, bahwa peluang kawan kita itu bercakap-cakap dengan wanita
meningkat.
Dari contoh di atas kita bisa merumuskan teorema Bayes secara umum.
Pernyataan
| Bagian ini memerlukan pengembangan |
Secara umum, teorema Bayes dinyatakan sebagai:
Dalam notasi ini P(A|B) berarti peluang kejadian A bila B terjadi dan P(B|A) peluang kejadian B bila A terjadi.
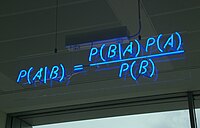





Komentar
Posting Komentar